Einfache lineare Regression

Was ist Regression?

Die Durchführung einer Regression (lat. regredi = zurückgehen) hat das Ziel, anhand von mindestens einer unabhängigen Variablen x (auch erklärende Variable genannt) die Eigenschaften einer anderen abhängigen Variablen y zu prognostizieren. Wenn die abhängige Variable nur von einer unabhängigen Variablen beschrieben wird, so spricht man von einer einfachen linearen Regression, wird sie von mehreren unabhängigen Variablen beschrieben, handelt es sich um eine multiple lineare Regression. Einige Beispielfragestellungen der Regression könnten wie folgt lauten:

• Der Leiter einer großen Möbelfirma möchte wissen, wie viel Geld er in die Werbung für sein Unternehmen investieren soll und ob diese sich in den Verkaufszahlen niederschlägt
• In Berlin soll im Auftrag des Polizeipräsidenten untersucht werden, ob eine höhere Präsenz der Polizei die Kriminalitätsrate senkt
• Der Schulleiter einer Privatschule ist daran interessiert, ob und in welchem Maße die Zahl der Anmeldungen für die erste Klasse sinken würden, wenn er 1000 Euro mehr an jährlichen Gebühren verlangt
• Ein Winzer möchte überprüfen, inwiefern das Wetter einen Einfluss auf die Qualität des gewonnenen Weines hat
• Eine Supermarktkette möchte herausfinden, wie viel ein Haushalt mit durchschnittlichem Einkommen pro Monat für Lebensmittel ausgibt
• Die Veranstalter eines jährlich stattfindenden Musikfestivals müssen vorhersagen, ob die Zahl der Festivalbesucher die nächsten zehn Jahre über mindestens konstant bleibt, damit sich die Investition in eine neue Bühnen- und Lichtanlage lohnt

Wie funktioniert Regression?

Die Genauigkeit der Prognose hängt bei einer Regression von der Korrelation bzw. der Stärke des linearen Zusammenhangs zwischen der unabhängigen und der abhängigen Variablen ab. Je höher die Korrelation, desto genauer ist die Prognose. Man kann den Zusammenhang visualisieren, indem man die Daten in einem Streudiagramm (engl.: "Scatterplot") darstellt, wie in Abbildung 1 zu sehen. Der Idealfall eines perfekten linearen Zusammenhangs, bei dem man exakt mithilfe des Wertes der unabhängigen Variable x den Wert der abhängigen Variable y vorhersagen kann, kommt in der Realität nicht vor. Die Datenpunkte bilden meist Wolken, aus welchen zwar ein positiver oder negativer Zusammenhang herausgelesen werden kann, eine genaue Aussage zu treffen ist jedoch rein visuell nicht möglich.

Abbildung 1

Aber wie kann nun eine möglichst genaue Prognose erstellt werden, wenn kein perfekter linearer Zusammenhang vorliegt? Man könnte frei Hand viele verschiedene Geraden durch die Datenwolke ziehen, die die Beziehung zwischen x und y beschreiben. Das Ziel ist aber, die beste Gerade zu finden, also diejenige, die den linearen Zusammenhang zwischen x und y am besten beschreibt. Die Methode der kleinsten Quadrate liefert die Lösung. Diese Methode bestimmt zu der Datenwolke die Gerade, welche die Summe der quadrierten Vorhersagefehler minimiert. So liefert die Methode der kleinsten Quadrate ein Schätzverfahren mit dem die Koeffizienten der sog. Regressionsgeraden, die den Zusammenhang zwischen x und y bestmöglich beschreibt, ermittelt werden können. Der Vorhersagefehler wird im Übrigen auch oft als Fehlerterm, Störgröße oder Residuum bezeichnet (Plural: Residuen).

Bezüglich der Interpretation von Zusamenhängen ist Vorsicht geboten: Ein linearer Zusammenhang zwischen zwei Variablen begründet noch keinen kausalen Zusammenhang. Zum Beispiel ist die Anzahl der Motorradunfälle positiv korreliert mit dem Auftreten von gutem Wetter, das bedeutet aber nicht, dass mehr Motorradunfälle geschehen, WEIL gutes Wetter ist.

Hinweis: Umgangssprachlich wird mit "schätzen" meist ein unsystematisches heuristisches Vorgehen beschrieben. Statistiker verstehen darunter jedoch ein systematisches Verfahren, mit dessen Hilfe im Kontext der Regression – durch die Methode der kleinsten Quadrate – die Koeffizienten der optimalen Regressionsgerade bestimmt werden.

Annahmen des einfachen linearen Regressionsmodells

Damit die Schätzung der Regressionsgeraden mit der kleinsten-Quadrate-Methode gewissen Optimalitätskriterien (s. Best Linear Unbiased Estimator, "BLUE") genügt, müssen einige Annahmen erfüllt sein:

• Die unabhängige Variable x hat einen linearen Einfluss auf y, dieser berechnet sich für jedes x durch . Der Index i zeigt an, dass es sich jeweils um einen bestimmten Wert i aus der Gesamtanzahl der Datenpunkte n handelt.
• 
  Der Erwartungswert des Vorhersagefehlers ist 0, äquivalent dazu ist der Erwartungswert von y . Das bedeutet, dass keinerlei Systematik in den Fehlern stecken sollte. Diese Annahme ist i.d.R. unproblematisch, solange das Modell die Konstante enthält.
• 
  Die Varianz des Vorhersagefehlers (und damit auch von y) ist konstant. Bei konstanter Varianz spricht man von Homoskedastizität, ist die Varianz nicht konstant, dann liegt Heteroskedastizität vor (Abbildung 2). Ist die Annahme der Homoskedastizität verletzt, können die kleinsten-Quadrate-Schätzer zwar noch verwendet werden, obwohl diese dann nicht mehr "optimale" Ergebnisse liefern.
• 
  Die Fehler sind unkorreliert. Diese Annahme kann bei Zeitreihen verletzt sein. Ihre Verletzung kann auch ein Symptom für einen nicht-linearen Zusammenhang zwischen x und y sein.
• Die unabhängige Variable x ist keine Zufallsvariable, außerdem muss x verschiedene Werte annehmen (also Varianz aufweisen). Eine optionale (!) Zusatzannahme ist, dass die Fehler normalverteilt sind mit Erwartungswert 0 und Varianz :
  Über diese Annahme gibt es in der Praxis viele Missverständnisse. Häufig wird behauptet, die Werte von y müssen einer Normalverteilung folgen (was so nicht stimmt). Darüber hinaus ist diese Annahme für die Schätzung der Koeffizienten nach der Methode der kleinsten Quadrate irrelevant. Sie wird lediglich benötigt, um Signifikanztests (z.B. ANOVA oder T-Test) sinnvoll interpretieren zu können.

Abbildung 2

Darstellung und Interpretation des einfachen linearen Regressionsmodells

Die geschätzte Regressionsgerade, die wir durch die Methode der kleinsten Quadrate erhalten haben, wird durch die folgende Gleichung beschrieben:

Die Dächer auf den Koeffizienten lassen erkennen, dass es sich um die Schätzwerte handelt.

Wer sich noch an den Mathematikunterricht erinnern kann, weiß, dass eine Gerade immer durch den Schnittpunkt mit der y-Achse (hier ) und den Anstieg (auch "Steigungskoeffizient", hier ) bestimmt wird. Nehmen wir wie anfangs als Beispiel erwähnt an, dass wir den linearen Zusammenhang zwischen den Ausgaben für Werbung und der Absatzmenge im Auftrag der Geschäftsführung einer Möbelfirma untersuchen wollen. Als abhängige Variable y steht die Absatzmenge auf der linken Seite der Gleichung, die unabhängige (oder auch erklärende) Variable x auf der rechten Seite ist die Summe, die für Werbung ausgegeben wurde. Sowohl Absatz wie auch Werbeausgaben wurden jeweils in 20 Filialen (i=1, 2, ..., 20) mit unterschiedlichen Einzugsgebieten erfasst. Um die Geradengleichung zu einem Regressionsmodell zu erweitern, fügen wir der Gleichung die Vorhersagefehler hinzu.

In diesem Regressionsmodell ist der Koeffizient der Schnittpunkt der geschätzten Regressionsgeraden mit der y-Achse, also der Punkt, wo ist. Das heißt nichts anderes, als dass der Wert die Menge an Absatz ist, die erzielt werden würde, wenn der Inhaber der Möbelfirma 0 Euro in Werbung investiert. Praktisch sollte bei der Interpretation von immer sehr vorsichtig vorgegangen werden, da um den Wert oft keine Datenpunkte existieren, die in die Berechnung der Regressionsgeraden mit einfließen könnten.

In sample vs. out of sample

Wenn das Verständnis eines Zusammenhangs im Vordergrund steht, interessiert uns bei der Regression nur der sog. "in sample"-Bereich, der von der Datenwolke abgegrenzt wird. Liegt der Fokus eher auf der Prognose, kann zusätzlich auch der Bereich außerhalb der Datenwolke ("out of sample") relevant werden. Dabei kann es passieren, dass der Zusammenhang außerhalb der Datenwolke nicht mehr linear ist. Ein Beispiel ist der Zusammenhang zwischen Körpergewicht und Größe bei erwachsenen Menschen (Abbildung 3). Die Datenwolke ist für die Variable x = Körpergröße begrenzt auf den Bereich zwischen 150 und 200 cm. Die Körpergrößen darunter stellen bei Erwachsenen eher eine Ausnahme dar und werden selten (oder in kleinen Stichproben gar nicht) beobachtet. So sollte man die Regressionsgerade unterhalb von 150 cm (out of sample) hier nicht einfach auch für die Interpretation des Zusammenhangs zwischen Körpergewicht und Größe bei Kindern verwenden, da sie ja nicht mit den entsprechenden Daten von Kindern berechnet wurde und somit auch nichts über diese aussagt. Genauso wenig Sinn macht in dem Fall auch die Interpretation von . Der Schnittpunkt der Regressionsgeraden mit der y-Achse ist im Beispiel aus Abbildung 3 weit im negativen Bereich. Demnach hätte ein Mensch, der 0 cm groß ist, ein negatives Körpergewicht (welches dem Achsenabschnitt der Geraden entspräche). Würden die Daten von Kindern in das Modell mit aufgenommen werden, ergäbe sich insgesamt ein nicht-linearer Zusammenhang zwischen Größe und Gewicht. Auch ohne diese zusätzliche Komplexität ist das in der Abbildung gezeigte Modell absolut brauchbar, solange sich die Interpretation auf den in-sample-Bereich beschränkt.

Abbildung 3

Der Koeffizient ist der Anstieg der Regressionsgeraden, welcher definiert ist als die Ableitung des Erwartungswertes von y nach x.

So gibt an, um wie viel die Absatzmenge sich verändert, wenn beispielsweise ein zusätzlicher Euro in Werbung investiert wird. Ein Euro ist in diesem Zusammenhang natürlich sehr wenig. Wird z.B. darüber nachgedacht, das Budget für Werbung um 10.000 Euro zu erhöhen, wäre der erwartete Effekt auf den Absatz . Zu beachten bleibt auch hier, dass der Zusammenhang out of sample anderen Regeln folgen kann (hier könnte z.B. ein Sättigungseffekt eintreten). Zuletzt bleibt noch der Vorhersagefehler . Da kein perfekter Zusammenhang zwischen dem Preis x und der Absatzmenge y vorliegt (dann wären alle ), benötigen wir den Fehlerterm im Regressionsmodell, der den Abstand zwischen dem tatsächlichen Wert () und dem von uns vorhergesagten Wert () misst. Der Vorhersagefehler steht ersatzweise für alle nicht beobachtbaren bzw. unberücksichtigten Variablen, die die Absatzmenge - neben dem Preis - noch beeinflussen. Ein Maß dafür, wie gut das gewählte Regressionsmodell ist, stellt das Bestimmtheitsmaß R² dar. Es gibt an, welcher Anteil der Variation von y durch unser Regressionsmodell erklärt wird. Näheres zum R² finden Sie in der Artikelserie über das Bestimmtheitsmaß R².

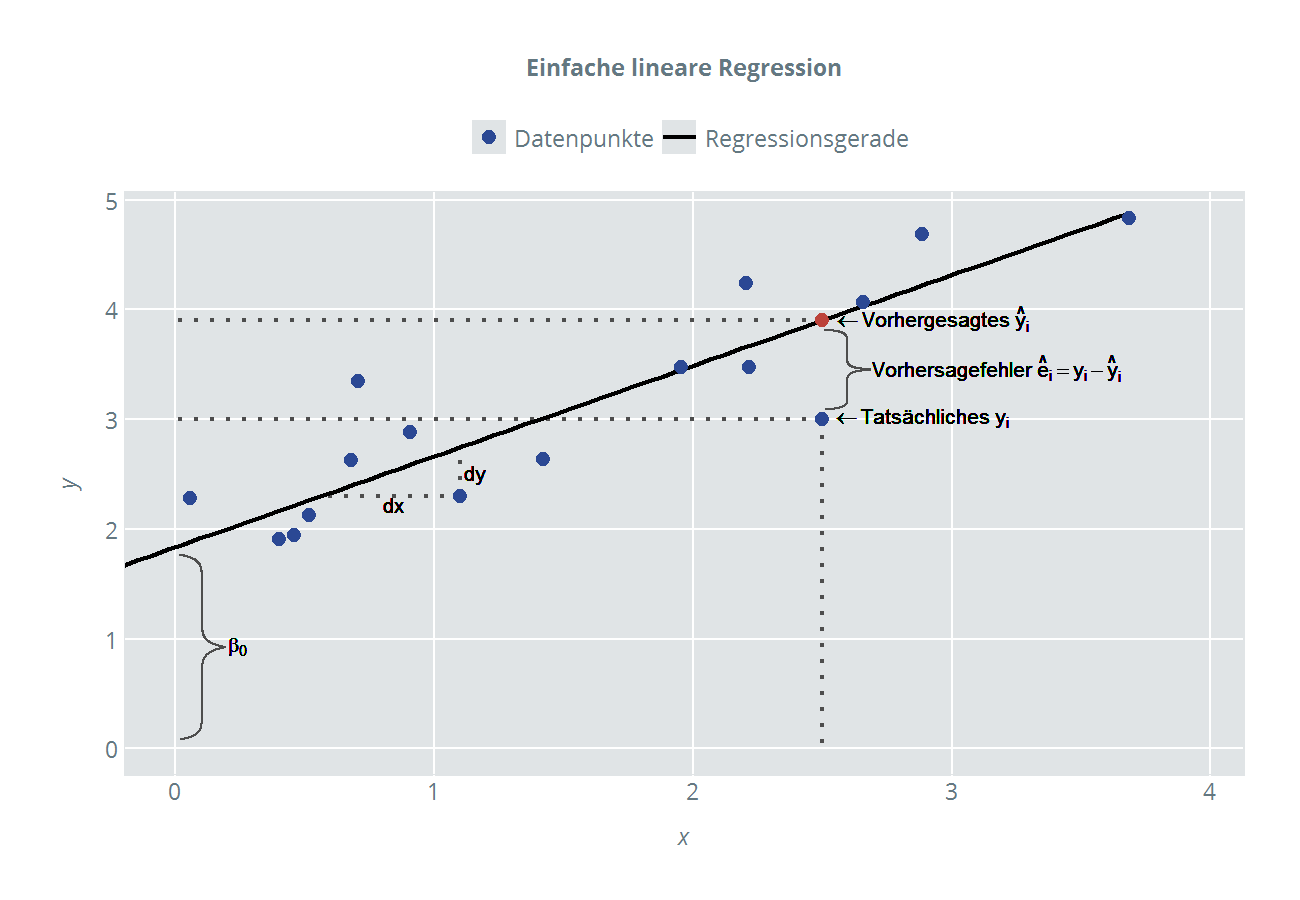Abbildung 4