Multiple lineare Regression
Im ersten Teil der Artikelserie (einfache lineare Regression) ging es um den Fall, dass die abhängige Variable y nur von einer erklärenden Variable x beeinflusst wird. In der Praxis sind die Zusammenhänge jedoch häufig komplexer und die abhängige Variable y wird durch mehrere Faktoren beeinflusst, so dass wir uns jetzt dem multiplen linearen Regressionsmodell zuwenden.
Multiples vs. multivariates Regressionsmodel
An dieser Stelle sei darauf hingewiesen, dass ein multiples und ein multivariates Regressionsmodell nicht das Gleiche sind. Ein multiples Regressionsmodell untersucht den Einfluss mehrerer unabhängiger Variablen xk auf eine abhängige Variable y. Bei einem multivariaten Modell gibt es mehrere abhängige Variablen. Es könnte z.B. simultan der Einfluss verschiedener erklärender Variablen auf den Umsatz und den Gewinn eines Unternehmens untersucht werden. Dabei würden zwei Modellgleichungen (eine für den Umsatz, eine für den Gewinn) simultan geschätzt werden. Weitere Informationen zum Thema multivariate Verfahren finden Sie hier.Darstellung und Interpretation des multiplen linearen Regressionsmodells
Die allgemeine Gleichung des Modells mit k erklärenden Variablen lautet
Interpretiert werden die Koeffizienten ähnlich wie beim einfachen linearen Regressionsmodell. Beim multiplen linearen Regressionsmodell ist jedoch nicht mehr der Schnittpunkt einer Regressionsgeraden mit der y-Achse. Durch die zusätzlichen unabhängigen Variablen wird durch die oben genannte Gleichung eine Hyperebene in einem k+1-dimensionalen Raum beschrieben. Ein visuelles Beispiel für ein Modell mit zwei unabhängigen Variablen ist in Abbildung 1 zu finden. kann als der Wert für y interpretiert werden, der sich einstellt, wenn alle unabhängigen Variablen gleich 0 sind. Die Koeffizienten der unabhängigen Variablen geben auch im multiplen linearen Regressionsmodell an, welchen Effekt eine Veränderung der entsprechenden Variable um eine Einheit auf den Erwartungswert von y hat (wenn alle anderen unabhängigen Variablen konstant gehalten werden). Ist der Wert des Koeffizienten beispielsweise -0.35, bedeutet das, wenn x3 um eine Einheit steigt, dass der Erwartungswert von y genau um den Wert 0.35 abnimmt. ist also gleich der partiellen Ableitung des Erwartungswertes von y nach x3:
Der Fehlerterm ist - wie im einfachen linearen Regressionsmodell - der Abstand zwischen dem geschätzten ŷi und dem tatsächlichen yi. Die Methode der kleinsten Quadrate lässt sich entsprechend analog im multiplen linearen Regressionsmodell zur Schätzung der Koeffizienten verwenden. Wie im Falle der einfachen Regression liefert diese Methode ein "optimales" Ergebnis (s. Best Linear Unbiased Estimator, "BLUE"), sofern einige Annahmen erfüllt sind.
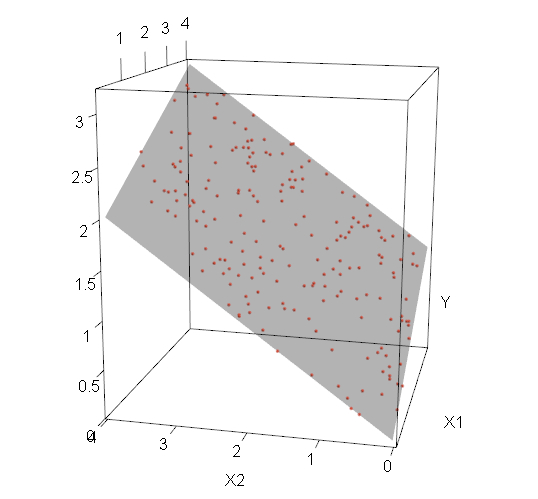 Abbildung 1
Abbildung 1
Annahmen des multiplen linearen Regressionsmodells
1. Die unabhängigen Variablen haben einen linearen Einfluss auf y
Ob diese Annahme verletzt ist, kann für jede einzelne erklärende Variable anhand eines Streudiagramms bzw. Residuenplots überprüft werden.
Was ist, wenn die Annahme eines linearen Zusammenhangs verletzt ist?
Wenn die Annahme des linearen Einflusses von x auf y erfüllt ist, sehen das Streudiagramm und der zugehörige Residuenplot in etwa folgendermaßen aus:

Im Residuenplot (rechts) sollten die Punkte unsystematisch streuen ("Weißes Rauschen", engl. "white noise"), d.h. dass es keine systematischen Strukturen in den Fehlern geben sollte.
Bei dem nächsten Beispieldiagramm ist die Annahme des linearen Einflusses von x auf y verletzt - stattdessen liegt ein quadratischer Zusammenhang vor.

Im Residuenplot (rechts) ist deutlich eine Tendenz zum Überschätzen bei kleineren und größeren Werten der abhängigen Variablen und eine Tendenz zum Unterschätzen im mittleren Bereich zu sehen. Abhilfe böte hier die Berücksichtigung der quadrierten Variable oder die Modellierung eines Splines bei komplizierteren Zusammenhängen.
2. Der Erwartungswert des Fehlerterms ist 0
Wie auch beim einfachen linearen Regressionsmodell ist der Erwartungswert des Fehlerterms 0, äquivalent dazu ergibt sich der Erwartungswert von y.
Diese Annahme ist i.d.R. unproblematisch, solange das Modell die Konstante β0 enthält.
3. Homoskedastie
Die Varianz von e und y wird als konstant, also homoskedastisch, angenommen.
Wie erkenne ich Heteroskedastie?
Einer Verletzung der Annahme der konstanten Varianz lässt sich anhand des Streudiagramms bzw. Residuenplots erkennen. Im folgenden Diagramm ist ein Modell mit heteroskedastischer Varianz dargestellt.

Was sind die Konsequenzen von Heteroskedastie in unserem Modell?
Die kleinsten-Quadrate-Schätzer können dann nicht mehr als die besten Schätzer angesehen werden. Vorsicht ist bei den Standardfehlern der Schätzer geboten, diese sind jetzt nicht mehr korrekt. Dieses Problem tangiert uns jedoch nur, wenn es um Konfidenzintervalle oder das Testen von Hypothesen geht. Als Abhilfe kann ein zweistufiges Schätzverfahren verwendet werden. Dabei wird zunächst "normal" geschätzt. Im Anschluss wird das Modell erneut geschätzt, wobei eine Fallgewichtigung eingeführt wird und jede Zeile ein Gewicht erhält, welches antiproportional zur Größe des zugehörigen geschätzten Residuums aus der ersten Stufe ist.
4. Die Kovarianz zwischen den einzelnen Fehlern ist 0.
Diese Annahme kann z.B. bei Zeitreihen verletzt sein oder auch ein Indiz für einen nicht-linearen Zusammenhang darstellen. Eng verwandt ist das "Endogenitätsproblem", bei dem ein Zusammenhang zwischen den Residuen und einer erklärenden Variable auftritt.
Das Endogenitätsproblem
Ist die Kovarianz zwischen der unabhängigen Variable x und dem Fehlerterm e nicht 0, d.h. wenn x und e miteinander korrelieren, dann spricht man von Endogenität. Es gibt u.a. folgende Ursachen für das Auftreten von Endogenität:
- Wichtige erklärende Variablen wurden nicht berücksichtigt (engl.: "omitted variables")
- Das Auftreten von simultaner Kausalität (mehrere Gleichungen beschreiben einen Zusammenhang)
- Messfehler in einer erklärenden Variable
- Unbeobachtete Heterogenität (sog. Individualeffekte)
- etc.
Was ist die Konsequenz von Endogenität?
Wenn das Endogenitätsproblem auftritt, sollte die Methode der kleinsten Quadrate nicht für die Schätzung verwendet werden. Um herauszufinden, ob überhaupt Endogenität im Modell vorliegt, kann auf den Hausman-Test zurückgegriffen werden. Ein Lösungsansatz besteht in der Verwendung sog. Instrumentvariablen (kurz: "IV"). Bei Individualeffekten liefert die Verwendung eines Paneldatenmodells konsistente Schätzungen.
5. Keine Multikollinearität
Die unabhängigen Variablen xk sind keine Zufallsvariablen und sie dürfen auch keine (exakten) linearen Funktionen einer jeweils anderen unabhängigen Variable sein.
Wenn es lineare Abhängigkeiten zwischen zwei oder mehr eklärenden Variablen gibt, spricht man von Multikollinearität. Je höher die Multikollinearität, desto instabiler wird das Modell. Ungewöhnlich hohe Standardfehler können ein Indiz für auftretende Multikollinearität sein. Diese führen zu einem Verlust an Signifikanz bei den statistischen Tests im Rahmen des Modells.
Was tun gegen Multikollinearität?
Über eine Korrelationsmatrix lassen sich die betroffenen Variablen i.d.R. leicht identifizieren. Ist dies geschehen, gibt es u.a. zwei Lösungsansätze:
- Lassen sich die erklärenden Variablen in einer solchen Gruppe inhaltlich ähnlich interpretieren und sind untereinander sehr hoch korreliert (Betrag der Korrelation nach Pearson >0.8 oder 0.9), kann eine Variable aus der Gruppe als "Proxy" ausgewählt werden, die stellvertretend für die Gruppe in das Modell aufgenommen wird. Beispiel: In einem Regressionsmodell für ein Callcenter werden als erklärende Variablen u.a. das monatliche Anrufvolumen eines Kunden, die Gesamtdauer der Anrufe und die monatliche Rechnungshöhe berücksichtigt. Alle drei Variablen korrelieren untereinander stark (Korrelation nach Pearson >0.9). Es wird nur eine Variable als Proxy für die "Nutzungsintensität" in das Modell aufgenommen.
- Führt der o.g. Ansatz nicht zum Erfolg (weil z.B. die Zusammenhänge komplexer sind oder die Korrelation zwischen den Variablen zu gering ist, so dass zu viel Information verloren ginge, wenn Variablen komplett entfernt würden), lassen sich Variablen evtl. mithilfe einer Hauptkomponenten- oder Faktorenanalyse zu einer geringeren Zahl an unkorrelierten Komponenten bzw. Faktoren zusammenfassen, die anstelle der ursprünglichen Variablen im Modell berücksichtigt werden.
6. Normalverteilung der Residuen (optional)
Die Normalverteilung der Residuen ist eine optionale Zusatzannahme.
Für die Methode der kleinsten Quadrate ist diese Annahme nicht erforderlich. Erst wenn Hypothesentests oder Konfidenzintervalle interpretiert werden sollen, ist die Normalverteilung der Residuen von Bedeutung. Wird ein Modell also lediglich zur Erstellung einer Prognose verwendet (wobei Hypothesentests keine Rolle spielen), ist diese Annahme vernachlässigbar. Wichtig ist auch, klarzustellen, dass sich die Normalverteilungsannahme auf die Residuen bezieht. In der Praxis trifft man häufig die (falsche) Meinung an, die Annahme müsse für die erklärenden Variablen oder die abhängige Variable gelten.
Wie lässt sich die Annahme überprüfen?
Die Residuen aus dem Modell können mittels eines QQ-Plots auf Normalverteilung überprüft werden. Bei ausreichender Fallzahl kann alternativ auch ein Test auf Normalverteilung (z.B. der Shapiro-Wilk-Test) durchgeführt werden.
Was tun, wenn die Residuen nicht normalverteilt sind, aber Signifikanztests relevant sind?
Gelegentlich löst sich das Problem durch die Aufnahme wichtiger bisher vernachlässigter erklärender Variablen in das Modell. Führt das nicht zum Erfolg, sollten noch einmal alle anderen Annahmen kritisch geprüft werden (insb. Linearität, Homoskedastizität und Unkorreliertheit). Besteht das Problem weiterhin, sollte überprüft werden, ob die Modellklasse korrekt gewählt ist. Die lineare Regression wird oft auch in Situationen verwendet, in der eigentlich andere Modelle zu bevorzugen wären. Ist die abhängige Variable z.B. eine Zählvariable, wäre eigentlich eine Poisson-Regression angebracht.








