Fehlende Werte Verstehen und Handhaben
Fehlende oder unvollständige Daten können sich sehr negativ auf jedes Data Science-Projekt auswirken. Dies ist besonders relevant für Unternehmen die sich in den frühen Phasen der Entwicklung solider Datenerfassungs- und -verwaltungssysteme befinden.
Während die beste Lösung für fehlende Werte darin besteht, sie zu vermeiden, indem gute Richtlinien für die Datenerfassung und -verwaltung entwickelt werden, bleibt uns letztendlich aber oft nichts anderes übrig als mit den Daten zu arbeiten, die uns zur Verfügung stehen.
Dieser Artikel behandelt die verschiedenen Arten fehlender Werte und Methoden um mit fehlenden Werten umzugehen. Diese Strategien reichen von einfachen Methoden - zum Beispiel der Auswahl von Modellen, die automatisch mit fehlenden Werten umgehen können, oder dem einfachen Löschen problematischer Beobachtungen - bis hin zu Methoden zur Schätzung der fehlenden Werte, was auch als Imputation bezeichnet wird.
Arten fehlender Werte
Missing Completely at Random (MCAR): In diesem Szenario stehen die fehlenden Werte in keinem Zusammenhang mit der untersuchten Beobachtung oder den anderen Variablen im Datensatz. Grundsätzlich gibt es keine systemischen Unterschiede zwischen den Beobachtungen mit und ohne fehlende Werte. Dies könnte beispielsweise der Fall sein, wenn einzelnen Umfrageteilnehmern nur eine Auswahl der Gesamtzahl möglicher Fragen angezeigt würde. Im Falle von MCAR können wir unsere Analysen einfach mit dem vollständigen Datensatz durchführen. MCAR-Daten sind jedoch in der Praxis sehr ungewöhnlich. Eine gute Faustregel lautet: Wenn Sie vorhersagen können, bei welchen Beobachtungen Werte fehlen (mit gesundem Menschenverstand, Regression usw.), handelt es sich nicht um MCAR.
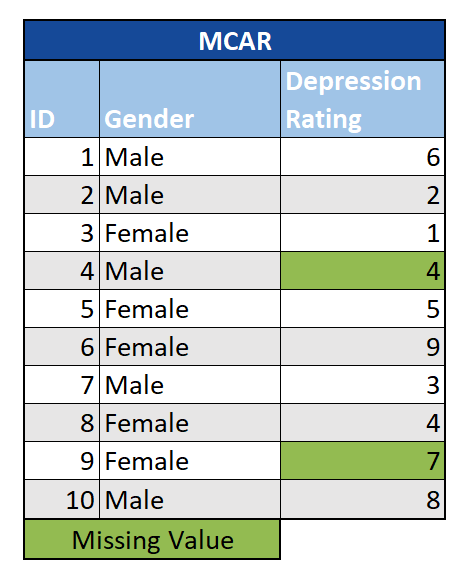
Missing at Random (MAR): In diesem Fall kann die Tatsache, dass Werte fehlen, anhand der anderen Variablen in der Studie vorhergesagt werden, nicht jedoch anhand der fehlenden Werte selbst. Nehmen wir zum Beispiel an, wir wissen, dass Männer in einer Umfrage weniger häufig Fragen zu Depressionen beantworten als Frauen. Wenn die Wahrscheinlichkeit, dass eine Person eine Frage zur Depression überspringt, nur mit ihrem Geschlecht zusammenhängt (was wir beobachten), nicht aber mit ihrem Depressionsgrad (der nicht beobachtet wird), können wir die Daten als MAR betrachten. Abhängig von der verwendeten Analysemethode können Datensätze mit MAR-Daten verzerrt sein. Daher müssen fehlende Werte frühzeitig im Prozess berücksichtigt werden.
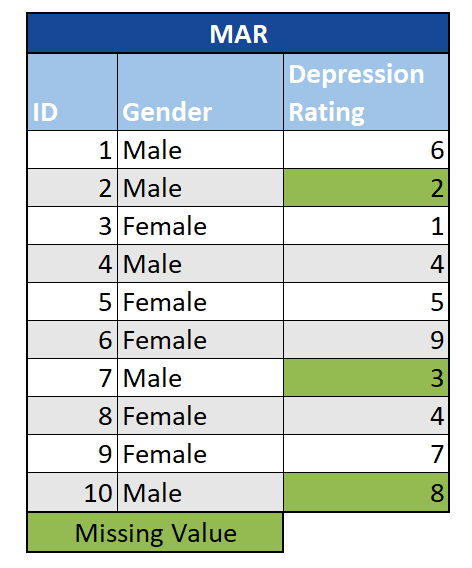
Missing Not at Random (MNAR): Bei MNAR-Daten hängt das Fehlen direkt mit dem Wert der fehlenden Beobachtung zusammen. Aufbauend auf dem obigen Beispiel wäre eine Umfrage zu Depressionen MNAR, wenn diejenigen mit besonders hohem Depressionsgrad die Beantwortung verweigern würden. Dies führt zu fehlenden Daten, die wir nicht ignorieren oder löschen können, ohne dass unsere Analyse verzerrt wird. Selbst die Imputation fehlender Werte kann zu irreführende Ergebnissen liefern. In schweren Fällen müssen wir möglicherweise eine bessere Strategie ausarbeiten und unsere Daten erneut erfassen.
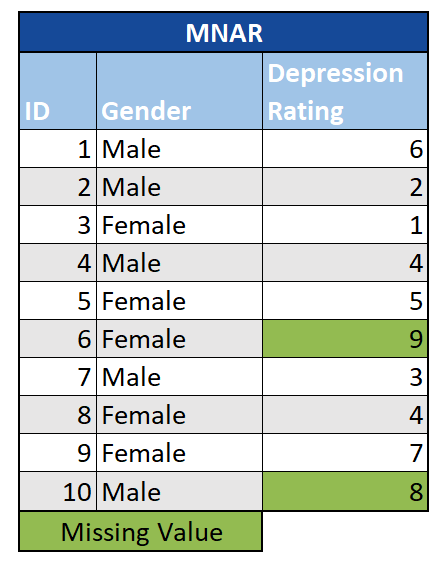
Methoden zum Umgang mit fehlenden Werten
Einfach ignorieren
Sofern man sich absolut sicher ist, dass die vorliegenden Daten MCAR sind, ist die beste und einfachste Lösung oft - wenn es auch albern klingt - die fehlenden Werte einfach zu ignorieren und einen Algorithmus zu wählen, der fehlende Werte automatisch verarbeiten kann. Beispielsweise entscheidet XGBoost für jede Probe über die beste Imputationsmethode, ohne dass zusätzliche Schritte erforderlich sind.
Löschen
Eine weitere Möglichkeit, mit fehlenden Werten umzugehen, besteht darin, problematische Beobachtungen oder Variablen zu löschen. Dies kann auf verschiedene Arten geschehen:
Listenweise: In diesem Szenario wird eine Beobachtung mit einem fehlenden Wert in einer Variablen vollständig entfernt. Das listenweise Löschen wird oft als „vollständige Fallanalyse“ bezeichnet und ist eine einfache Lösung, wenn nur wenige Beobachtungen mit MCAR-Werten bei einer ansonsten großen Stichprobengröße vorliegen. Wenn die Stichprobengröße jedoch klein ist oder die Daten nicht MCAR sind, kann das listenweise Löschen zu einer Verzerrung der Analyse führen.
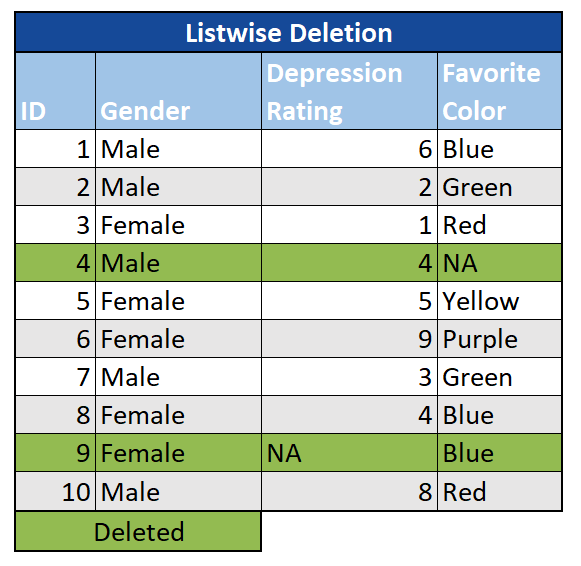
Paarweise: Wir können auch Fälle mit MCAR-Daten für die Variablen, an denen wir interessiert sind, weglassen, jedoch nicht für andere Analysen. In diesem Fall betrachten wir Teilmengen der Daten mit vollständigen Fällen, wodurch im Vergleich zum listenweisen Löschen mehr Informationen erhalten bleiben. Da sich die Stichproben während Ihrer Studie unterscheiden, wird die Interpretation jedoch zu einer Herausforderung.
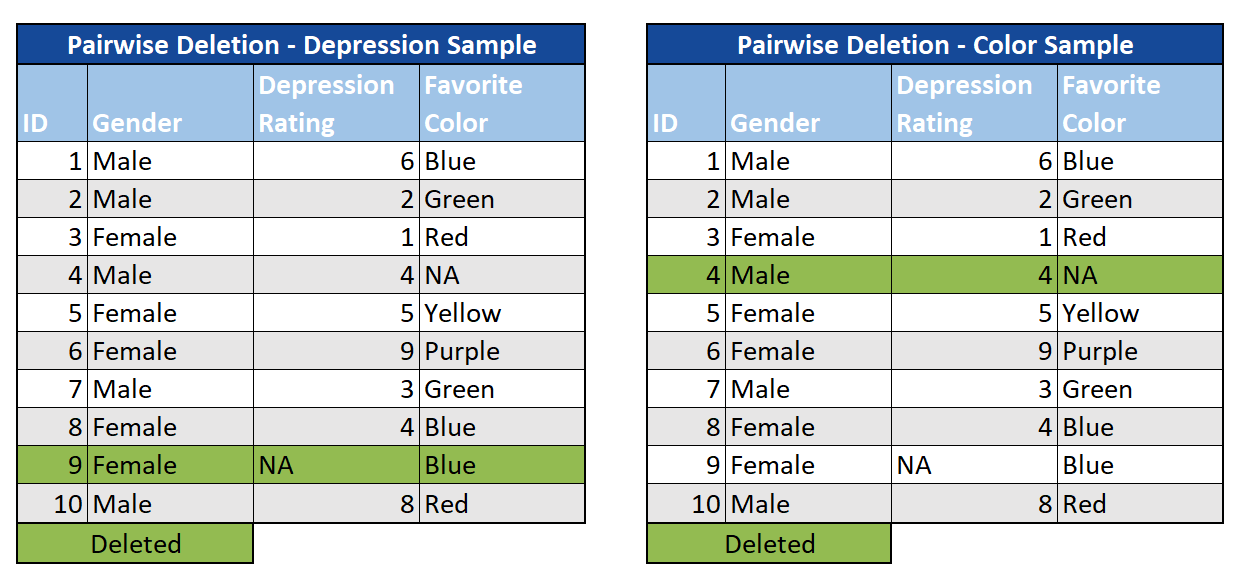
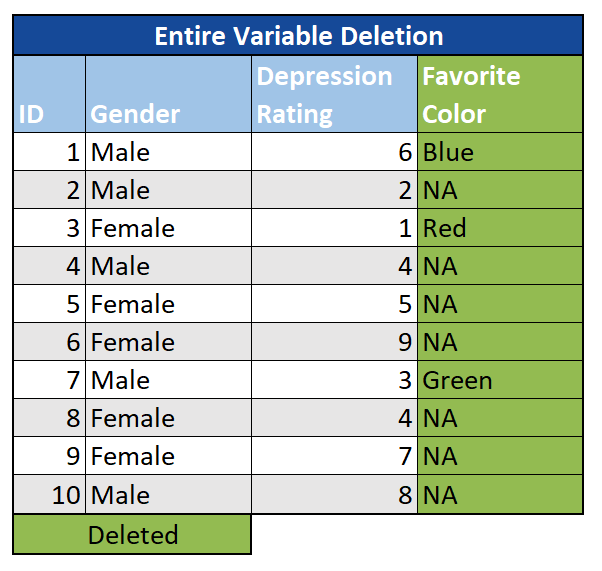
Ganze Variablen: Eine letzte Option besteht darin, eine gesamte Variable (Spalte) aus der Analyse wegzulassen. Es gibt zwar keine Faustregel, wann dies geschehen sollte, aber in Situationen, in denen eine große Datenmenge fehlt (z. B. 60% +) und die Variable unbedeutend ist, kann es bei Bedarf eine Option sein, sie einfach auszuschließen.
Imputation
Die Imputation - oder das Ausfüllen fehlender Werte gemäß einer Regel - ist normalerweise die beste Strategie für den Umgang mit fehlenden Werten. Es gibt viele Möglichkeiten, dies zu erreichen, von einfach bis komplex. Einige mögliche Optionen werden folgend betrachtet:
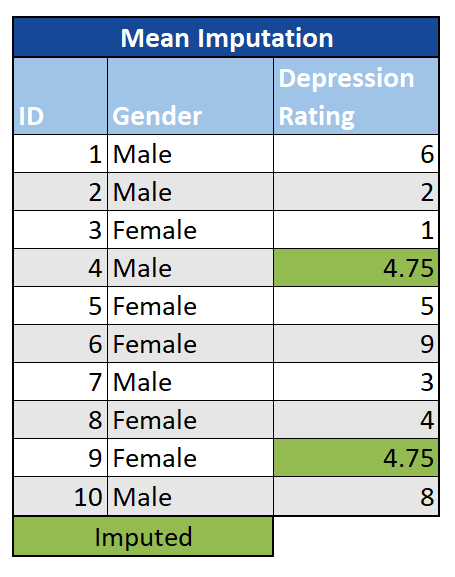
Mittelwert / Median / Modus: Die einfache Verwendung des Mittelwerts oder Medians anstelle des fehlenden Werts ist eine einfache Methode zur Imputation. Dies funktioniert, indem der Mittelwert oder Medianwert in einer bestimmten Spalte berechnet und dann die fehlenden Daten durch diesen Wert ersetzt werden. Ein ähnlicher Ansatz für kategoriale Daten besteht darin, Fehler durch den häufigsten Wert (Modus) zu ersetzen. Dies kann entweder für den gesamten Datensatz oder für eine Teilmenge erfolgen (z. B. indem zuerst nach Alter oder Geschlecht geschichtet und dann der Mittelwert für die entsprechende Teilstichprobe berechnet wird). Neben der Einfachheit besteht ein wesentlicher Vorteil darin, dass bei der mittleren Imputation der Stichprobenmittelwert für die unterstellten Daten gleich bleibt. Aus der Stichprobentheorie wissen wir auch, dass die Verwendung des Mittelwerts als angenommenen Wert sinnvoll ist, da der Mittelwert eine vernünftige Schätzung für zufällig ausgewählte Beobachtungen mit normalverteilten Daten darstellt. Ein wesentlicher Nachteil besteht jedoch darin, dass die Varianz im Datensatz verringert und die Kovarianz zwischen den verbleibenden Variablen verzerrt wird.
K Nearest Neighbors (KNN): KNN ersetzt fehlende Werte, indem es die k ähnlichsten Beobachtungen findet (auf der Grundlage eines Abstandsmaßes) und den Mittelwert / Median / Modus dieser Nachbarn nimmt. Diese Methode erfordert die Bestimmung der geeigneten Anzahl der zu berücksichtigenden Nachbarn sowie die Frage, wie die „Entfernung“ am besten gemessen werden sollte. KNN funktioniert sowohl für kontinuierliche als auch für kategoriale Daten gut, und seine nicht parametrische Natur kann sehr nützlich sein, wenn die Daten einem ungewöhnlichen Muster folgen. Ein Nachteil des Algorithmus besteht jedoch darin, dass er ziemlich rechenintensiv ist und sich nicht gut für hochdimensionale Daten eignet, bei denen es kaum Unterschiede zwischen dem nächsten Nachbarn und dem am weitesten entfernten gibt.
Lineare Regression: Die lineare Regression kann fehlende Werte ersetzen, indem die vorhandenen Variablen verwendet werden, um eine Vorhersage über den fehlenden Wert zu treffen. Ein Nachteil bei diesem Verfahren besteht darin, dass die Standardfehler reduziert werden, da die imputierten Werte von anderen Variablen vorhergesagt werden. Außerdem muss davon ausgegangen werden, dass zwischen den Variablen im Datensatz eine lineare Beziehung besteht, was möglicherweise nicht der Fall ist.
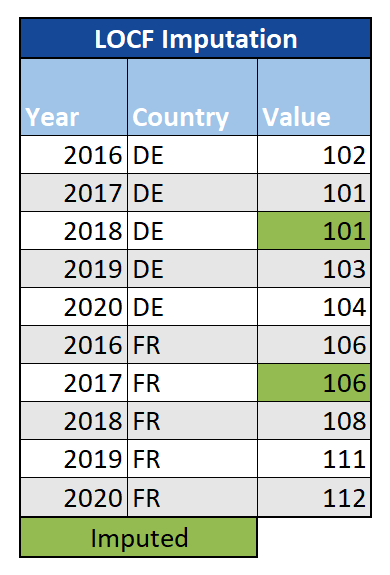
Last Observation Carried Forward (LOCF)/Next Observation Carried Backward (NOCB): Für Zeitreihendaten besteht eine einfache Option darin, den zuletzt beobachteten Wert für fehlende Daten zu verwenden. In ähnlicher Weise könnten wir die erste Beobachtung nach dem fehlenden Wert verwenden, der als Next Observation Carried Backward (NOCB) bezeichnet wird. Diese Methoden sind zwar leicht zu kommunizieren und zu verstehen, berücksichtigen jedoch Schwankungen im Zeitverlauf möglicherweise nicht angemessen.
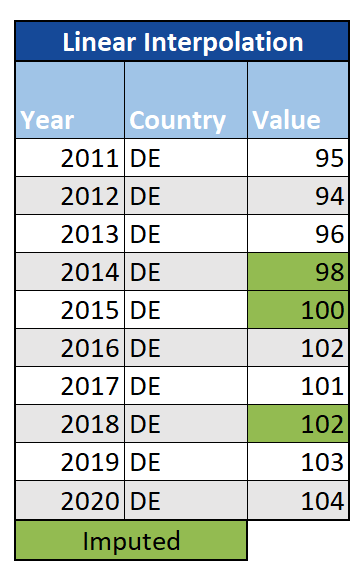
Lineare Interpolation: Eine weitere Option für Zeitreihendaten ist die lineare Interpolation, bei der fehlende Werte gefüllt werden, indem die Beobachtungen sowohl vor als auch nach ihnen berücksichtigt werden (z. B. indem der Mittelwert genommen wird oder indem die Differenz zwischen den vorherigen und nächsten Beobachtungen gleichmäßig in so viele Werte aufgeteilt wird, wie fehlende Werte aufgefüllt werden müssen). Dies kann zwar eine Verbesserung gegenüber LOCF und NOCB darstellen, ist jedoch möglicherweise nicht ausreichend, wenn der Trend der Daten besonders komplex ist, und eignet sich nicht für saisonale Daten.
Multiple Imputation by Chained Equations (MICE): Bei der multiplen Imputation wird die Verteilung der beobachteten Daten berücksichtigt und mehrere plausible Schätzungen für den fehlenden Wert erstellt. Mehrere Datensätze werden einzeln erstellt und analysiert, um einen Satz von Parameterschätzungen zu erhalten. Diese Methode berücksichtigt die Unsicherheit bei den fehlenden Werten besser und kann sowohl kontinuierliche als auch kategoriale Daten effektiv verarbeiten.
Dies ist natürlich keine vollständige Liste, und es gibt viele andere Imputationsmethoden (z. B. Imputation mit Random Forests, GANs, usw.). Es gibt grundsätzlich keine pauschale Lösung für den Umgang mit fehlenden Werten. Vielmehr ist es wichtig, die Art der Daten und der fehlenden Werte zu berücksichtigen, um eine fundierte Entscheidung darüber zu treffen, wie der Lösungsweg aussehen sollte.