Multi-Armed Bandits als Alternative zum A/B-Test
Heutzutage sind die meisten Personen mit dem Konzept des A/B-Testens vertraut. Es handelt sich dabei um eine der am häufigsten verwendeten Methoden um Werbeentscheidungen zu treffen, dies gilt insbesondere für den Bereich Online Marketing. In einem A/B-Test werden die Kunden in zwei oder mehr Gruppen geteilt, denen jeweils verschiedene Versionen vorgelegt werden (beispielsweise eines speziellen Angebots oder eines Layouts einer Werbekampagne). Am Ende des Testes wird die daraus hervorgehende erfolgreichste Variante für alle Kunden fortgesetzt.
Zwar hat sich diese Methode bewährt, jedoch gibt es spezielle Situationen, in denen sie nicht die ideale Wahl darstellt. Zum Beispiel ist es für die Integrität des Experiments wichtig, dass die Ergebnisse des A/B-Testes nicht während der laufenden Testphase überprüft werden. Doch was geschieht, wenn sich eine der getesteten Varianten als besonders schlecht oder außerordentlich gut herausstellt? Das bedeutet, dass ein Teil der Kunden nicht optimal bedient werden kann.
Gibt es nur einen Test, sind die Opportunitätskosten dieser Methode vermutlich zumutbar und die Investition, um die bestmögliche Variante zu finden, ist es wahrscheinlich wert. Allerdings wird im Falle, dass viele Varianten getestet werden, ein größerer Teil der Kunden über eine längere Zeit mit einer suboptimalen Variante bedient, was in signifikanten Kosten resultieren kann.
In einer idealen Welt würden wir in der Lage sein, schlecht performende Varianten sehr schnell auszuschließen und nur für solche einen vollen A/B-Test durchführen, die Erfolg versprechend sind bzw. bereits bewiesen haben, dass sie erfolgreich(er) sind.
Multi-Armed Bandits als Lösung
Die Spielautomaten die durch das Ziehen eines Hebels bedient werden, tragen den Namen „einarmige Banditen“, da sie die Bankkonten der Spieler leerräumen. Der Name „Mehrarmiger Bandit“ wurde durch die Idee inspiriert, an mehreren Spielautomaten mit jeweils verschiedenen unbekannten Erfolgsraten zeitgleich zu spielen. In diesem Szenario wird es unser Ziel als Spieler sein, herauszufinden, welche Maschine den höchsten Erfolg verspricht und an dieser entsprechend häufiger als an anderen zu spielen, um den Gewinn zu maximieren.
Während es so scheint, als wäre unser Ziel ausschließlich an der Maschine mit dem höchsten Erfolg zu spielen, es sei denn wir kennen im Voraus zuverlässig die exakten Erfolgsquoten (was wir in diesem Szenario nicht tun), würden wir tatsächlich so lange an den anderen Maschinen weiterspielen wollen, bis wir sicher sind, dass wir die beste Maschine gewählt haben.
Dies bringt uns dem Konzept des Exploration- vs. Exploitation-Trade-Offs näher (“Learn or earn“). Hierbei geht es grundsätzlich um den Trade-Off zwischen späterer (Exploration) oder direkter (Exploitation) Belohnung.
Ein A/B-Test ist rein exploratorisch: Kunden werden zufällig einer Variante zugewiesen und der erreichbare Erfolg ist einfach der durchschnittliche Erfolg aller Varianten (was bedeutet, dass dieser immer geringer als der Erfolg der stärksten Variante sein wird). Hierbei findet keine bewusste Exploitation einer erfolgreicheren Variante statt, was zu „Bedauern“ führt: der Unterschied zwischen der optimalen Strategie, die wir wählen würden, wenn wir den wahren Erfolg kennen würden und der getätigten Handlung.
Bandit-Algorithmen dagegen versuchen die Balance zwischen Exploration und Exploitation zu finden, indem sie jede Variante ausreichend explorieren, um die stärkste zu finden und vor allem anschließend die optimale Handlung zu nutzen, um den gesamten Gewinn zu maximieren. Der Algorithmus untersucht darüber hinaus andere mögliche Varianten um herauszufinden, ob sie in Zukunft stärker werden. Die Idee ist es, mit einem höheren finalen Gewinn zu enden (und dementsprechend mit geringerem „Bedauern“) und gleichzeitig dem Algorithmus die Möglichkeit zu geben, Daten über andere Varianten zu sammeln.
Arten von Multi-Armed Bandit-Algorithmen
Es gibt viele Arten von Bandit-Algorithmen. Drei der am häufigsten verwendeten – Epsilon Greedy, Upper Confidence Bounds und Thompson Sampling werden in diesem Artikel behandelt, um zu illustrieren, wie diese Algorithmen in der Praxis funktionieren.
Epsilon Greedy
Nach einer initialen Anzahl von rein exploratorischen Versuchen werden beim Epsilon Greedy- (oder auch ε-Greedy) Algorithmus in ε*100 Prozent der Zeit zufällige Hebel gezogen. Den Rest der Zeit (1- ε) wird der Hebel mit dem höchsten bekannten Erfolg gezogen. Wenn wir beispielsweise ε auf 0.10 setzen, wird der Algorithmus 10 % der Zeit zufällige Alternativen explorieren und 90 % der Zeit wird er die Variante nutzen, die den höchsten Erfolg aufweist. Wir können den ε-Greedy-Algorithmus erweitern, indem der Wert von ε über die Zeit reduziert wird, wodurch die Möglichkeit zur weiteren Exploration begrenzt wird, sobald wir den Erfolg von jedem Hebel kennen. Dies wird als Decayed Epsilon Greedy bezeichnet.
Upper Confidence Bounds
Die Familie der Upper Confidence Bounds (UCB) Algorithmen basiert auf dem Prinzip des Optimismus unter Unsicherheit, welches annimmt, dass die unbekannten Erfolge jedes Hebels so hoch sind, wie es laut der beobachtbaren Daten möglich ist. UCB-Algorithmen explorieren zunächst zufällig, um ein Verständnis der wahren Wahrscheinlichkeit in Bezug auf den Erfolg eines Hebels zu bekommen. Anschließend fügt der Algorithmus denjenigen Hebeln einen „Explorationsbonus“ hinzu, bei denen er sich unsicher ist. Diese Hebel werden solange priorisiert, bis der Algorithmus sich sicherer hinsichtlich des Erfolges des Hebels ist. Dieser Explorationsbonus verringert sich mit jeder Runde, ähnlich wie beim Decayed Epsilon Greedy.
Thompson Sampling
Es ist möglich, dass ein erfolgreicher Hebel zunächst schwach erscheint und dadurch von einem Greedy-Algorithmus nicht ausreichend exploriert wird, um den wahren Erfolg zu bestimmen. Thompson Sampling ist eine bayesianische Alternative. Bei diesem Algorithmus wird eine Wahrscheinlichkeitsverteilung der wahren Erfolgsrate für jede Variante, basierend auf den Ergebnissen, die bereits gezeigt wurden, bestimmt. Für jeden neuen Versuch wählt der Algorithmus die Variante basierend auf einer Stichprobe der A-posteriori-Wahrscheinlichkeit des größten Erfolges. Der Algorithmus lernt daraus und bringt damit letztendlich die Erfolgsraten der Stichprobe näher an die wahren Erfolgsraten heran.
Simulation
Verwenden wir zur Illustration ein vereinfachtes Beispiel, um einen traditionellen A/B-Test mit Epsilon Greedy und Thompson Sampling zu vergleichen. In diesem Szenario kann einem Kunden eine von fünf Varianten einer Werbung gezeigt werden. Für unsere Zwecke nehmen wir an, dass Werbung 1 mit einer Conversion-Rate von 5% am schlechtesten abschneidet. Jede Werbung funktioniert 5 % besser als die letzte, wobei Werbung 5 mit einer Conversion-Rate von 25 % die erfolgreichste Werbung darstellt. Wir führen 1000 Versuche durch, was bedeutet, dass in einer idealen Welt die Anzahl der Conversions, die wir erhalten können, wenn wir ausschließlich die optimale Werbung zeigen bei 250 liegt (gegeben einer 25%igen Conversion-Rate bei 1000 Versuchen).
Im traditionellen A/B-Test wird jede Werbung initial gleich häufig präsentiert. Nach einer gewissen Zeit (in unserem Fall nach der Hälfte der 1000 Versuche) wird die erfolgreichste Werbung (bzw. die erfolgreichsten Werbungen) durch das Durchführen eines statistischen Signifikanztests isoliert und solche Werbungen entfernt, die signifikant schlechter als die Top Performer abschneiden. Von nun an werden nur diese übrig gebliebenen Werbungen gezeigt.
# A/B TEST
# setup
horizon <- 1000L
simulations <- 1000L
conversionProbabilities <- c(0.05, 0.10, 0.15, 0.20, 0.25)
nTestSample <- 0.5 * horizon
clickProb <- rep(NA, simulations)
adDistMatrix <- matrix(NA, nrow = simulations,
ncol = length(conversionProbabilities))
adDistMatrixAB <- matrix(NA, nrow = simulations,
ncol = length(conversionProbabilities))
# simulation
for(i in 1:simulations){
testSample <- sapply(conversionProbabilities,
function(x) sample(0:1, nTestSample, replace = TRUE, prob = c(1 - x, x)))
testColumns <- (1:length(conversionProbabilities))[-which.max(colSums(testSample))]
p.values <- sapply(testColumns, function(x) prop.test(x = colSums(testSample[, c(x, which.max(colSums(testSample)))]),
n = rep(nTestSample, 2))$p.value)
adsAfterABTest <- (1:length(conversionProbabilities))[- testColumns[which(p.values < 0.05)]]
# now just with the best performing ad(s)
ABSample <- sapply(conversionProbabilities[adsAfterABTest],
function(x) sample(0:1,
round((horizon - nTestSample) * length(conversionProbabilities) /
length(adsAfterABTest), 0),
replace = TRUE, prob = c(1 - x, x)))
clickProbTest <- sum(as.vector(testSample)) / length(unlist(testSample))
clickProbAB <- sum(as.vector(ABSample)) / length(unlist(ABSample))
clickProb[i] <- clickProbTest * (nTestSample / horizon) + clickProbAB * (1 - nTestSample / horizon)
# distribution of which ads were seen over the course of all trials
adDistMatrix[i,] <- rep(1 / length(conversionProbabilities), length(conversionProbabilities))
adDistributionAB <- rep(0, length(conversionProbabilities))
adDistributionAB[adsAfterABTest] <- rep(1 / length(adsAfterABTest), length(adsAfterABTest))
adDistMatrixAB[i,] <- adDistributionAB
}
# total payoff
ABPayoff <- (nTestSample * clickProbTest) + (nTestSample * clickProbAB)
Der A/B-Test resultiert in einem Gesamterfolg von 187.4 Conversions bei 1000 Versuchen, was circa 75% des möglichen Erfolges entspricht. Wir können außerdem visualisieren, welche Werbungen gesehen wurden, um ein besseres Verständnis des Prozesses zu bekommen.
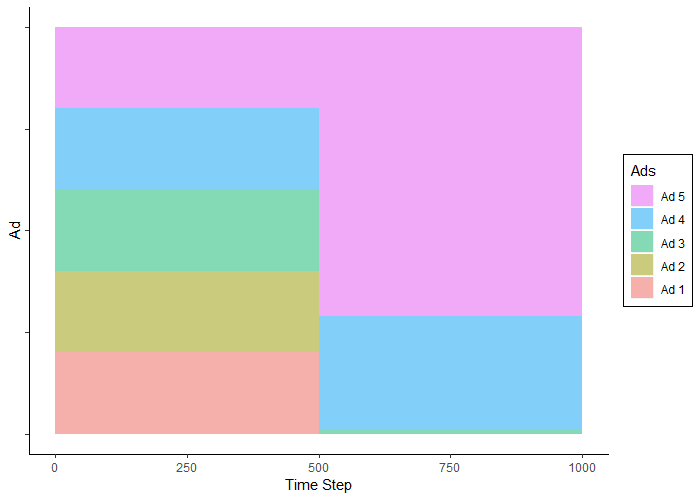
Wie erwartet wurden die Werbungen während der ersten 500 Versuche im gleichen Verhältnis gesehen. In den nächsten 500 Trials wurde Werbung 5 (die erfolgreichste Werbung) am häufigsten gesehen, gefolgt von Werbung 4 und nur sehr selten Werbung 3.
In der nächsten Simulation können wir das contextual Paket nutzen, um uns einen Epsilon Greedy Algorithmus mit ε = 0.10 anzuschauen. Das bedeutet, dass der Algorithmus nur 10 % der Zeit zufällig exploriert und 90 % der Zeit exploitiert.
library(contextual)
# EPSILON GREEDY
horizon <- 1000L
simulations <- 1000L
conversionProbabilities <- c(0.05, 0.10, 0.15, 0.20, 0.25)
bandit <- BasicBernoulliBandit$new(weights = conversionProbabilities)
policy <- EpsilonGreedyPolicy$new(epsilon = 0.10)
agent <- Agent$new(policy, bandit)
historyEG <- Simulator$new(agent, horizon, simulations)$run()
plot(historyEG, type = "arms",
legend_labels = c('Ad 1', 'Ad 2', 'Ad 3', 'Ad 4', 'Ad 5'),
legend_title = 'Epsilon Greedy',
legend_position = "topright",
smooth = TRUE)
summary(historyEG)
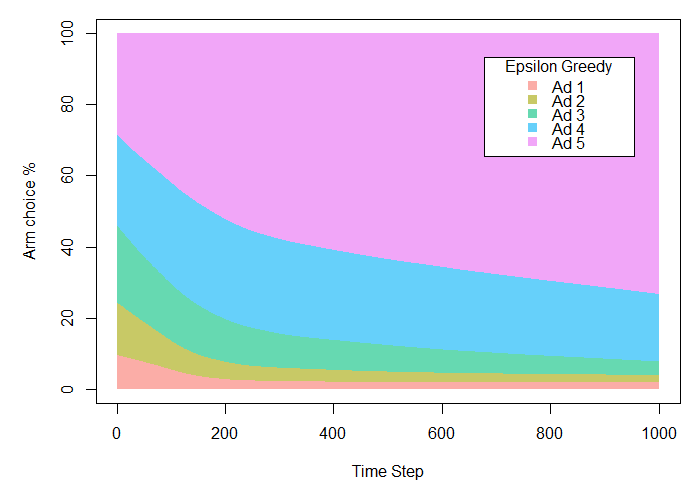
Hier können wir sehen, dass der Epsilon Greedy Algorithmus sehr schnell fähig ist, zu erkennen, dass Werbung 5 den anderen überlegen ist und sich über die Zeit verbessert. Der Gesamterfolg beträgt 217.11 Conversions und liegt damit bei 87 % des möglichen Erfolges. Das ist circa 14 % höher als beim A/B-Test, da der Algorithmus in der Lage ist, die erfolgreichste Werbung sehr viel schneller zu nutzen als traditionelle Methoden.
Nun können wir beide Beispiele mit dem Thompson Sampling vergleichen, indem wir auch hierbei das contextual Packet nutzen.
# THOMPSON SAMPLING
horizon <- 1000L
simulations <- 1000L
conversionProbabilities <- c(0.05, 0.10, 0.15, 0.20, 0.25)
bandit <- BasicBernoulliBandit$new(weights = conversionProbabilities)
policy <- ThompsonSamplingPolicy$new(alpha = 1, beta = 1)
agent <- Agent$new(policy, bandit)
historyThompson <- Simulator$new(agent, horizon, simulations)$run()
plot(historyThompson, type = "arms",
legend_labels = c('Ad 1', 'Ad 2', 'Ad 3', 'Ad 4', 'Ad 5'),
legend_title = 'Thompson Sampling',
legend_position = "topright",
smooth = TRUE)
summary(historyThompson)
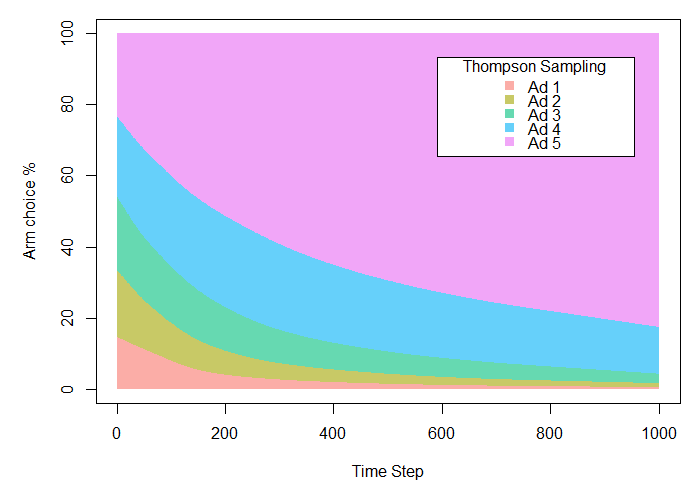
Es zeigt sich, dass Thompson Sampling das erfolgreichste Modell mit einer Erfolgsrate von 219.97 (fast 88% der möglichen Conversions) darstellt. Das sind nahezu 16% mehr als mit dem traditionellen A/B-Test.
Darüber hinaus scheinen die Ergebnisse zunächst nicht allzu verschieden von denen des Epsilon Greedy Beispiels zu sein. Es ist jedoch wichtig anzumerken, dass sich dies mit weiteren Trials ändern würde. Da Epsilon Greedy dazu verpflichtet ist, 10% der Zeit des gesamten Experiments zu explorieren, besteht ein Limit hinsichtlich der Optimierung für den Algorithmus. Thompson Sampling ist dahingehend nicht beschränkt und kann stattdessen die erfolgreichste Option nutzen, sobald diese bestimmt wurde.
Insgesamt können Bandit-Algorithmen eine ausgezeichnete Lösung für viele Anwendungsfälle bieten. Im Wesentlichen stellen sie eine „leichte“ Form des Reinforcement Learnings dar, bei der der Algorithmus ohne Wissen über die Aufgabe im Voraus auto-optimiert und sich Feedback aus der Umwelt holt. Reinforcement Learning und dessen Anwendung für das Online Marketing werden in einem zukünftigen Blogartikel diskutiert.
