Text Mining – Part 1: Analyse der Wahlprogramme für die BTW 2017
In diesem Artikel werden die aktuellen Wahlprogramme der Fraktionen CDU/CSU, SPD, Grüne, Linke, AfD und FDP zur Bundestagswahl am 24. September 2017 in Deutschland mittels Text Mining in R untersucht. Dabei wird analysiert, welche Wörter wie häufig in den Wahlpogrammen auftauchen, aber auch, wie wichtig diese sind. Die Methodologie folgt dem Buch Text Mining with R von Julia Silge und David Robinson.
Die folgenden Analysen basieren auf bereits vorbereiteten Daten, die im R-Objekt txt abgespeichert sind. Dieses enthält die Spalten words und party. Kommt ein Wort im Programm einer Partei mehrfach vor, so taucht auch die entsprechende Zeile mehrfach in den Daten auf. Dabei wurden irrelevante Wörter (z.B. “und”, “so”), Parteinamen und Synonyme der Parteinamen bereits heraus gefiltert.
Eine detaillierte Beschreibung der Datenvorbereitung findet sich im zweiten Teil der Serie.
# Pakete laden
library("cowplot")
library("dplyr")
library("forcats")
library("ggplot2")
library("tidytext")
# Parteinamen und dazugehörige Farben für Plots
partyColor <- c(AfD = "#2B4894",
CDU = "black",
FDP = "#DD9123",
Grüne = "#93BB51",
Linke = "#8A3B89",
SPD = "#cd5364")
Die 20 häufigsten Begriffe
Die 20 häufigsten Wörter über alle Wahlprogramme hinweg – also ohne Berücksichtigung der Partei – sind in folgendem Barplot zu finden:
txt %>%
count(words, sort = TRUE) %>%
head(n = 20) %>%
mutate(words = reorder(words, n)) %>%
ggplot(aes(words, n)) +
geom_col() +
labs(x = NULL,
y = "Anzahl",
title = "Häufigste Begriffe (alle Parteien)") +
coord_flip()
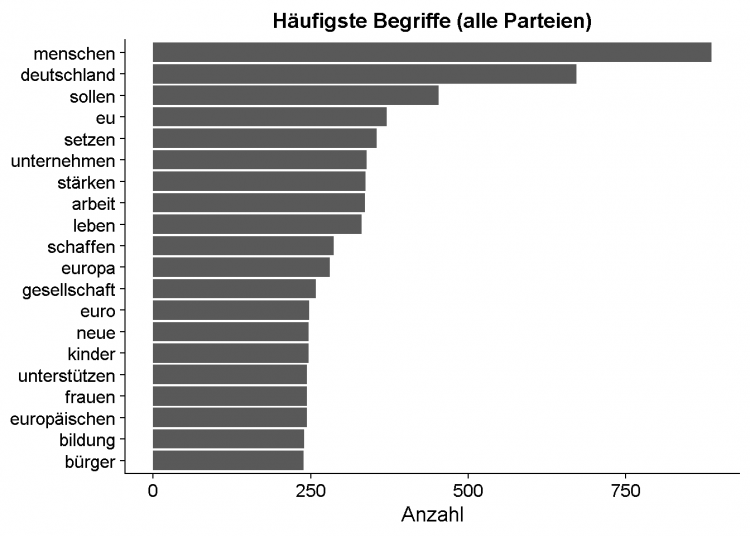
Die 20 häufigsten Begriffe je Partei
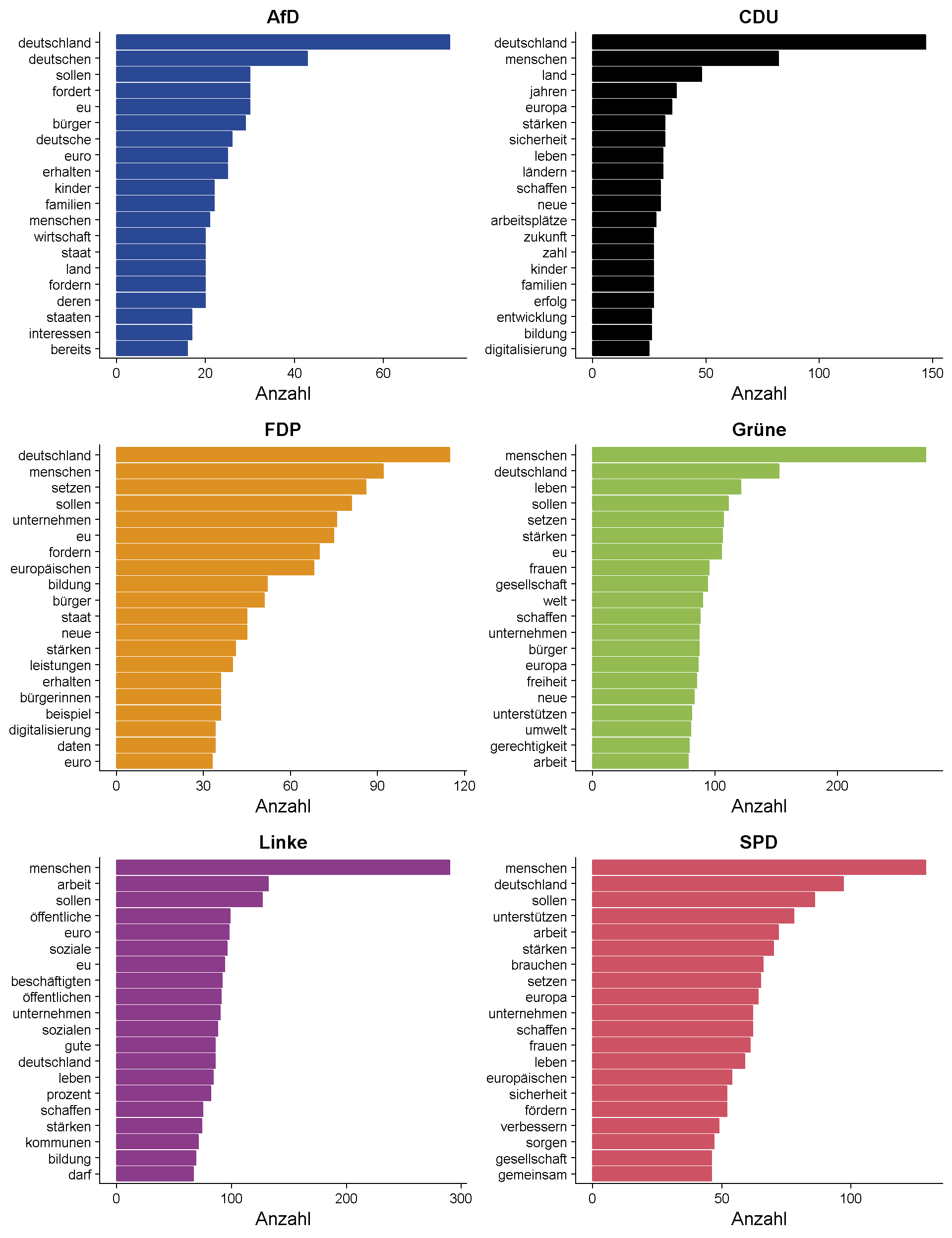
Zusätzlich ist von Interesse, welche Begriffe in den Programmen der einzelnen Parteien besonders häufig auftauchen. Der folgende Plot zeigt dazu die zwanzig häufigsten Wörter je Partei.
plot <- lapply(names(partyColor), function(p) {
txt %>%
filter(party == p) %>%
count(words, sort = TRUE) %>%
head(n = 20) %>%
mutate(words = reorder(words, n)) %>%
ggplot(aes(words, n)) +
geom_col(fill = partyColor[p], color = partyColor[p]) +
labs(y = "Anzahl", x = NULL, title = p) +
theme(axis.text = element_text(size = 10)) +
coord_flip()
})
plot_grid(plotlist = plot, nrow = 2, ncol = 3, align = "hv")
Die wichtigsten Begriffe
Wie wichtig ein Wort in einem Text ist, hängt nicht nur von seiner Häufigkeit in diesem Text ab, sondern auch davon, wie oft es üblicherweise verwendet wird. Dies wird bei der tf-idf-Methode berücksichtigt. Dabei wird ein Text immer im Kontext einer Sammlung von Texten betrachtet:
The idea of tf-idf is to find the important words for the content of each document by decreasing the weight for commonly used words and increasing the weight for words that are not used very much in a collection or corpus of documents …. Calculating tf-idf attempts to find the words that are important (i.e., common) in a text, but not too common. (Silge and Robinson, 2017)
Ein Wort im Wahlprogramm ist also dann wichtig für dieses Wahlprogramm, wenn es dort häufig, aber im Vergleich dazu in den anderen Programmen weniger häufig auftaucht.
Im Folgenden berechnen wir das tf-idf-Maß für alle Wörter in den verschiedenen Wahlprogrammen. Es resultiert eine Tabelle, die für verschiedene Parteien und Wörter die Auftretenshäufigkeit sowie die Ausprägungen auf den Maßen tf (Häufigkeit im Wahlprogramm der Partei), idf (inverse Häufigkeit in den anderen Programmen) und tf_idf (Maß für die Wichtigkeit) enthält.
# Häufigkeit der Wörter nach Partei
wrdCount <- txt %>%
count(party, words, sort = TRUE) %>%
ungroup
# Wortanzahl nach Partei
ttlWords <- wrdCount %>%
group_by(party) %>%
summarise(total = sum(n))
wrdCount <- left_join(wrdCount, ttlWords, by = "party")
# Berechnung des tf-idf-Maßes
wrdCount <- wrdCount %>%
bind_tf_idf(words, party, n)
# Ausgabe
wrdCount %>%
select(-total) %>%
arrange(desc(tf_idf))
## # A tibble: 41,877 x 6
## party words n tf idf tf_idf
## <chr> <chr> <int> <dbl> <dbl> <dbl>
## 1 AfD fordert 30 0.0035100035 0.6931472 0.002432949
## 2 FDP weltbeste 22 0.0012867755 1.7917595 0.002305592
## 3 Grüne kopf 57 0.0018490884 1.0986123 0.002031431
## 4 Grüne herzen 56 0.0018166483 1.0986123 0.001995792
## 5 AfD volk 8 0.0009360009 1.7917595 0.001677089
## 6 CDU wahlperiode 14 0.0014521315 1.0986123 0.001595330
## 7 Grüne sinn 66 0.0021410498 0.6931472 0.001484063
## 8 AfD bevölkerungsentwicklung 7 0.0008190008 1.7917595 0.001467452
## 9 AfD lehnt 11 0.0012870013 1.0986123 0.001413915
## 10 AfD parteienfinanzierung 6 0.0007020007 1.7917595 0.001257816
## # ... with 41,867 more rows
Mit einem Plot lassen sich die Daten für die 25 wichtigsten Wörter visualisieren:
plotwrds <- wrdCount %>%
arrange(desc(tf_idf)) %>%
mutate(words = factor(words, levels = rev(unique(words))))
plotwrds %>%
top_n(25) %>%
ggplot(aes(words, tf_idf, fill = party), color = NA) +
geom_col() +
labs(x = NULL, y = "tf-idf", fill = "Partei",
title = "Wichtigste Begriffe (alle Parteien)") +
coord_flip() +
scale_fill_manual(breaks = names(partyColor), values = partyColor)
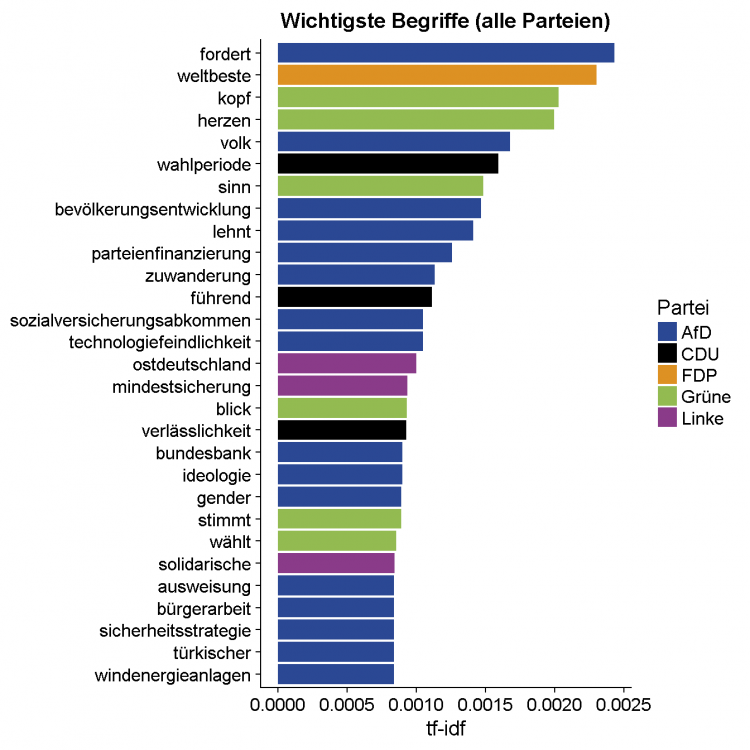
Das Wahlprogramm der AfD enthält besonders viele Wörter, die einen hohen tf-idf-Wert aufweisen; die SPD hingegen taucht in diesem Plot gar nicht auf. Deswegen betrachten wir im nächsten Abschnitt die wichtigsten Wörter nach Partei.
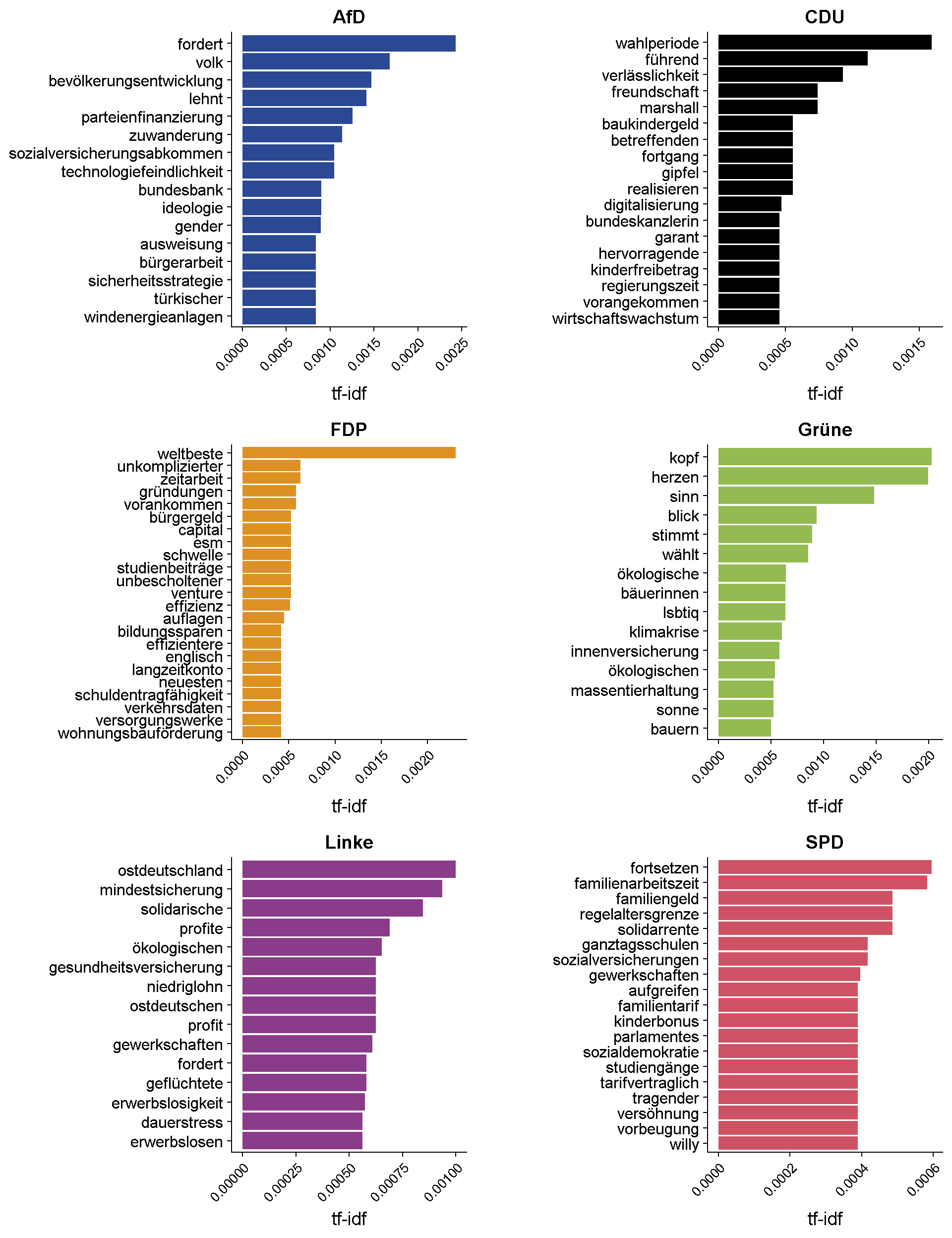
Die wichtigsten Wörter je Partei
Der folgende Plot zeigt für alle Parteien jeweils die 15 wichtigsten Wörter. Falls mehrere Wörter gleich wichtig sind, tauchen möglicherweise auch mehr als 15 Wörter im Plot auf.
plot <- lapply(names(partyColor), function(p) {
plotwrds %>%
filter(party == p) %>%
top_n(15, tf_idf) %>%
mutate(words = fct_reorder(words, tf_idf)) %>%
ggplot() +
geom_col(aes(words, tf_idf), show.legend = FALSE, fill = partyColor[p]) +
labs(x = NULL, y = "tf-idf", title = p) +
coord_flip() +
theme(axis.text.x = element_text(angle = 45, hjust = 1, size = 10))
})
plot_grid(plotlist = plot, nrow = 3, ncol = 2, align = "hv")
Zipf’s Law
Je häufiger ein Wort im Text auftaucht, desto niedriger ist sein Rang, wenn man alle Wörter nach Häufigkeit sortiert – das ist nicht überraschend. Doch es geht noch weiter:
Zipf’s law states that the frequency that a word appears is inversely proportional to its rank. … Classic versions of Zipf’s law have frequency ∝ 1/rank. (Silge and Robinson, 2017)
Das heißt also, dass sich aus dem bloßen Häufigkeitsrang eines Wortes in einem Wahlprogramm bereits (ungefähr) ableiten lässt, wie oft dieses Wort im gesamten Text auftritt. Der folgende Plot stellt den Zusammenhang zwischen der relativen Worthäufigkeit und dem Häufigkeitsrang dar. Die Achsen sind dabei logarithmiert.
# relative Worthäufigkeit und Häufigkeitsrang
frqByRank <- wrdCount %>%
group_by(party) %>%
mutate(rank = row_number(),
`term frequency` = n / total) %>%
ungroup
# lineares Modell mit logarithmierten Werten zum Einzeichnen einer Regressionsgerade
lm <- lm(log10(`term frequency`) ~ log10(rank), data = frqByRank)
frqByRank %>%
ggplot() +
geom_line(aes(x = rank, y = `term frequency`, color = party),
size = 1.2, alpha = 0.8) +
geom_abline(intercept = lm$coefficients["(Intercept)"],
slope = lm$coefficients["log10(rank)"],
color = "gray50",
linetype = 2) +
scale_x_log10() +
scale_y_log10() +
scale_color_manual(breaks = names(partyColor), values = partyColor) +
labs(x = "Häufigkeitsrang", y = "Relative Worthäufigkeit", color = "Partei")
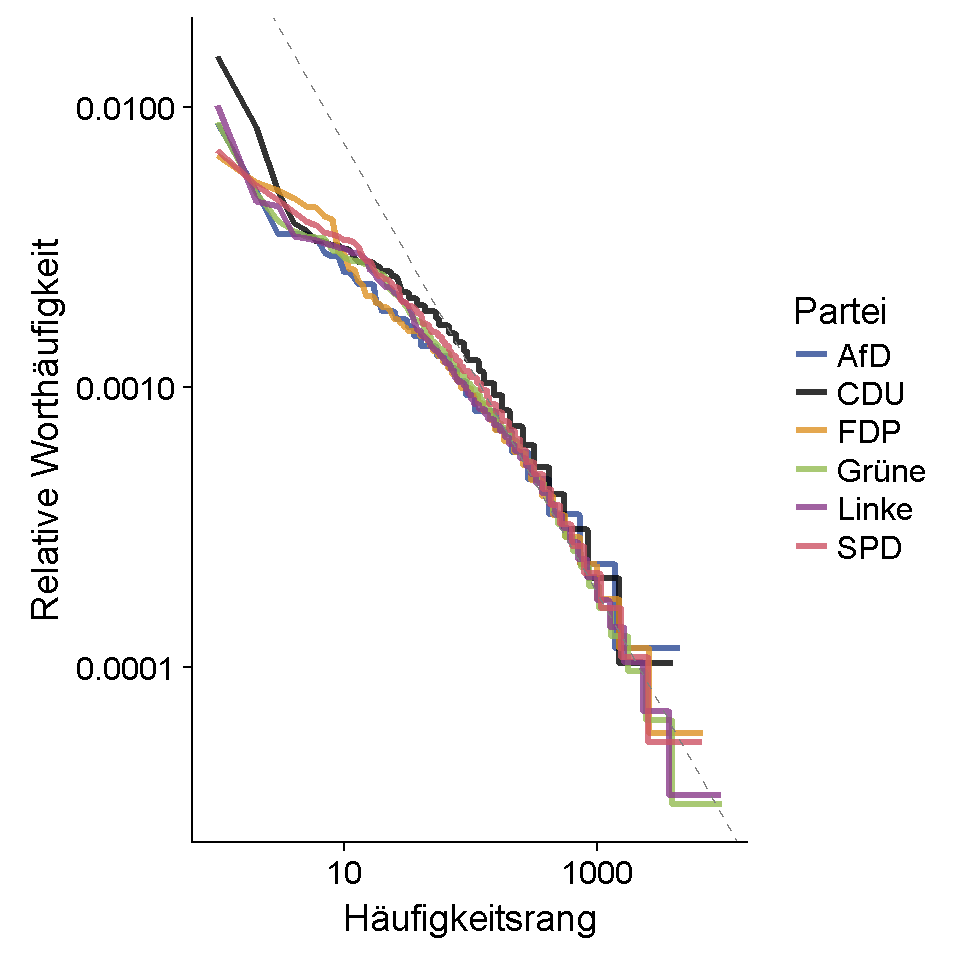
Für mittelhäufige oder seltenere Wörter (d.h. mittlere und hohe Ränge) stimmen Vorhersage und tatsächlicher Verlauf der Linien ungefähr überein. Bei sehr hohen Worthäufigkeiten (d.h. niedrigen Rängen) hingegen ergibt sich eine Abweichung von der Vorhersage von Zipf’s Law. Die Wörter aus den obersten Häufigkeitsrängen sind demnach etwas seltener als zu erwarten.
Quelle
Silge, Julia, and David Robinson. 2017. “Text Mining with R: A Tidy Approach”. O’Reilly Media, Inc, USA

