Business Case: Datenvisualisierung
Data Visualization: Räumliche Verteilung der Bundestagswahlergebnisse
Task
Das Amt für Statistik Berlin-Brandenburg beabsichtigte für Berlin bereits in der Wahlnacht eine grafische Analyse der Bundestagswahlergebnisse 2017 durchzuführen. Dabei war insbesondere von Interesse, wo innerhalb Berlins Parteien besonders stark oder besonders schwach abgeschnitten haben. Die räumliche Verteilung der jeweiligen Stimmanteile soll dabei möglichst fein aufgelöst - unabhängig von der Zusammenfassung zu Wahlbezirken - dargestellt werden. Der klassische Ansatz sind sogenannte Choroplethen- oder Flächenwertstufenkarten, welche die Stimmanteile für jeden Wahlbezirk farblich klassiert in einer Karte darstellen:
Choroplethenkarte: Prozentualer Anteil der Stimmen der Wähler*innen für die Linke
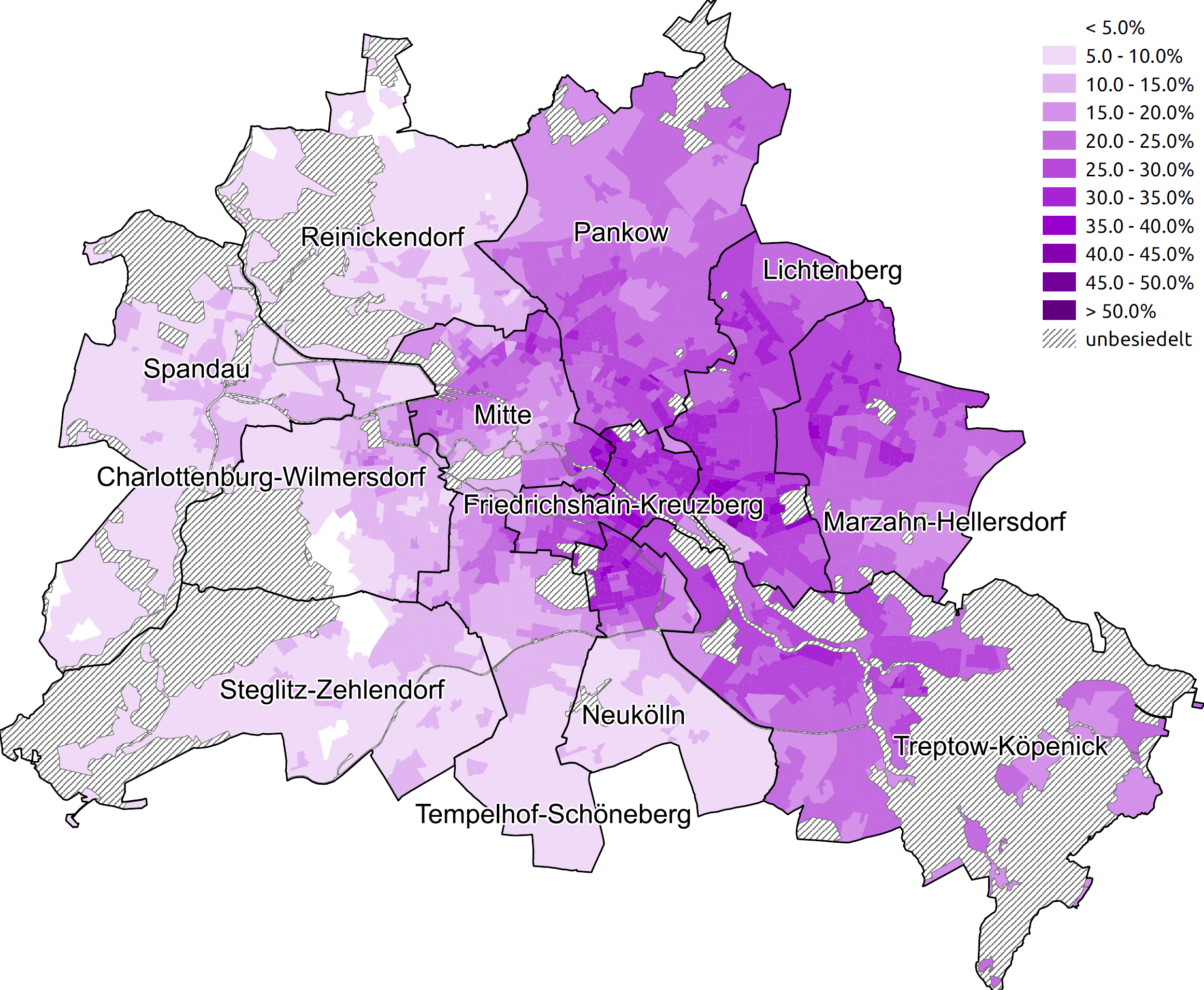 Kartenberechnung und -erstellung Kerstin Erfurth, EMOS-Studierende, Freie Universität Berlin und Amt für Statistik Berlin-Brandenburg
Kartenberechnung und -erstellung Kerstin Erfurth, EMOS-Studierende, Freie Universität Berlin und Amt für Statistik Berlin-Brandenburg
Diese Darstellungsform weist jedoch mehrere Nachteile auf. So werden Gebiete, in diesem Fall Wahlbezirke, als farblich einheitlich dargestellt, was sie aber häufig nicht sind. Außerdem führen die unterschiedliche Größe und teilweise verschlungene Form der Wahlbezirke zu visuellen Verzerrungen. Durch die klassierte Darstellung gehen dazu noch Informationen verloren, da bereits geringe Veränderungen zu einer anderen Einfärbung der Karte führen, was insbesondere bei einem Vergleich über die Zeit problematisch ist. Gesucht war ein Verfahren das diese Nachteile nicht besitzt. Die sogenannte Methode der Kerndichteschätzung ermöglicht eine räumlich glatte Schätzung über die Wahlbezirke und grafische Darstellung der Analysefragestellung. Die innovative Methode namens Kernelheaping, die es ermöglicht dieses Verfahren auch auf räumlich zusammengefasste Daten anzuwenden, wurde von Dr. Marcus Groß (INWT), Prof. Dr. Timo Schmid (FU Berlin) und Prof. Dr. Ulrich Rendtel (FU Berlin) entwickelt.
Data
Grundlage der Analyse sind die Auszählungsergebnisse der Bundestagswahl 2017 in Berlin, diese liegen für die Urnenwahlbezirke und die Briefwahlbezirke vor. Für die Nachnutzung wurden die Daten und die Geometrien vom Amt für Statistik Berlin-Brandenburg in das Open Data-Portal daten.berlin.de eingestellt.
Analytics
Das Kernelheaping-Verfahren ermöglicht es Anteile (z.B. Stimmanteile) aufgrund von Daten, die für Teilflächen (z.B. Wahlbezirke) zusammengefasst wurden, zu schätzen. Im Zuge dieses Verfahrens wird ein SEM-Algorithmus (Stochastic Expectation Maximization) angewandt, welcher in einem iterativen Verfahren sogenannte Pseudo-Stichproben erzeugt. Diese bilden die Basis für die eigentliche Schätzung. Das gleichnamige R-Paket zur Methodologie wurde von Dr. Marcus Groß entwickelt und online auf CRAN frei zur Verfügung gestellt. Als neues Feature wurden nicht bewohnte Gebiete wie der Tiergarten, Grunewald oder das Tempelhofer Feld in der Schätzung ausgeschlossen. Nähere Hinweise zur Methodik und zur Umsetzung mit R gibt es demnächst auf unserem Blog.
Solution
Das neuartige Verfahren Kernelheaping ermöglicht neue Einblicke in die räumliche Verteilung der Stimmen von Wähler*innen. Mit dieser Darstellungsform sind die Hochburgen der einzelnen Parteien innerhalb Berlins für den Betrachter wesentlich besser sichtbar als mit herkömmlichen Choroplethenkarten, da sie nicht mehr von der Struktur der Wahlbezirke abhängig ist. Choroplethenkarten geben bei einer groben Auflösung, z.B. auf Bezirksgrenzen, die räumlichen Unterschiede sehr ungenau wieder. Dagegen liefert eine sehr hohe Auflösung ein unbrauchbar verrauschtes Bild. Die der Kernelheaping-Methode zugrunde liegende Kerndichteschätzung hingegen liefert einen optimalen Ausgleich zwischen den beiden Extremen. Das Amt für Statistik konnte mit dem Verfahren noch in der Wahlnacht Kerndichtekarten der Wahlergebnisse herstellen und kurzfristig publizieren.
Prozentualer Anteil der Stimmen der Wähler*innen für die Linke
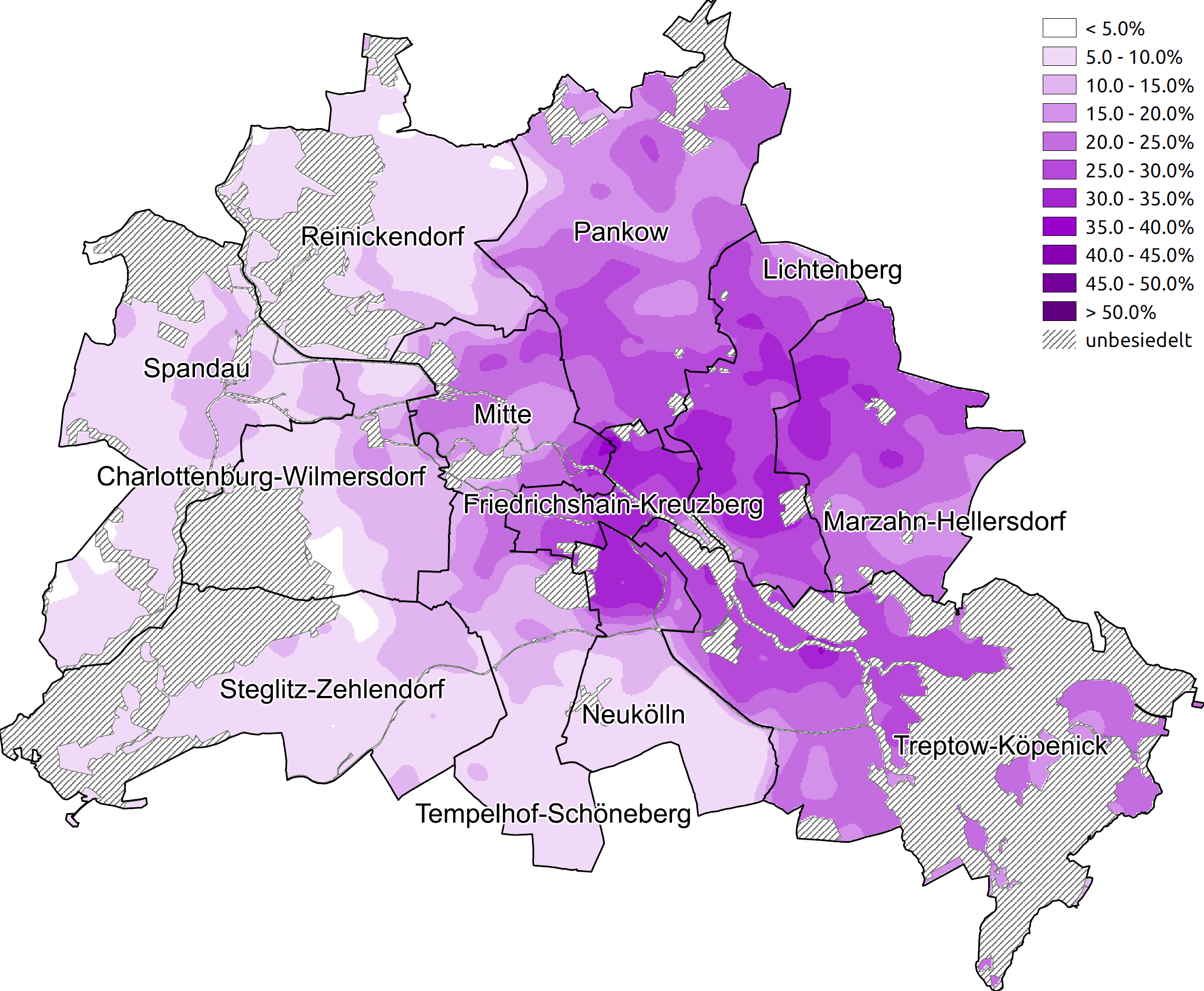 Kartenberechnung und -erstellung Kerstin Erfurth, EMOS-Studierende, Freie Universität Berlin und Amt für Statistik Berlin-Brandenburg
Kartenberechnung und -erstellung Kerstin Erfurth, EMOS-Studierende, Freie Universität Berlin und Amt für Statistik Berlin-Brandenburg
Links
- Blogartikelserie zum begleitenden R Paket Kernelheaping
- Amt für Statistik Berlin-Brandenburg
- Bericht der Landeswahlleiterin: Wahl zum 19. Deutschen Bundestag am 24. September 2017, S. 67-71
- Wahlergebnisse für Berlin
- Öffentlich verfügbares R-Paket Kernelheaping
- Forschungsartikel: doi:10.1111/rssa.12179
- Freie Universität Berlin
- European Master in Official Statistics (EMOS)